Graham's Number angka terbesar di dunia

 

Bilangan Graham (Ronald Graham), adalah suatu bilangan sangat besar yang merupakan batas atas pada solusi permasalahan tertentu dalam teori Ramsey.
Bilangan tersebut mengundang perhatian lebih ketika Martin Gardner mendeskripsikannya dalam sesi “Mathematical Games” pada Scientific American, pada bulan November 1977, menuliskan bahwa “Dalam sebuah pembuktian yang belum dipublikasikan, Graham telah membuat … sesuatu sehingga memegang rekor bilangan terbesar yang pernah digunakan dalam pembuktian matematis serius.”

1980 Guinness Book of World Records mengulang perkataan Gardner, menambah popularitas pada bilagan ini. bilangan Graham tak terbayangkan lebih besar dari bilangan besar lainnya yang terkenal, seperti googol, googolplex, dan sekaligus lebih besar dari bilangan Skewes dan bilangan Moser. Lingkup semesta sekalipun jauh lebih kecil untuk memuat representasi digit biasa untuk bilangan Graham, asumsikan tiap digit memakai sekurang-kurangnya satu volume Planck. Sekalipun “menara” pangkat berbentuk tidak berguna untuk keperluan ini, meskipun dapat dideskripsikan dengan rumus rekursif secara mudah menggunakan notasi panah-atas Knuth (lihat definisinya di sini) atau secara ekivalen, seperti yang dilakukan Graham. Sepuluh digit terakhir bilangan Graham adalah …2464195387.
Bilangan bulat tertentu yang diketahui jauh lebih besar dari bilangan Graham telah muncul dalam banyak pembuktian matematis serius (mis. dalam hubungan dengan variasi bentuk tentu Friedman pada teorema Kruskal).
Graham’s problem
Bilangan Graham dihubungkan dengan persoalan berikut dalam cabang matematika yang dikenal sebagai teori Ramsey:

Pada n-dimensional hypercube, hubungkan tiap pasang verteks untuk memperoleh graf lengkap pada 2ⁿ verteks. Lalu warnai tiap sisi graf ini merah atau biru. Berapa nilai terkecil n dimana setiap pewarnaan berisi setidaknya satu subgraf lengkap planar 4-verteks warna-tunggal?

Graham & Rothschild (1971) membuktikan bahwa persoalan ini mempunyai sebuah solusi, N*, dan diberikan sebagai rentang perkiraan 6 ≤ N* ≤ N, dengan batas atas N adalah bilangan tertentu yang didefinisikan secara eksplisit dan sangat besar. Dalam notasi panah-atas Knuth, . Batas bawah 6 sudah kemudian diperbaiki menjadi 11 oleh Geoff Exoo, Indiana State University (2003). Maka, perkiraan batasan eksplisit yang dikenal untuk solusi N* adalah 11 ≤ N* ≤ N.
Subjek artikel sekarang ini adalah batas atas G yang jauh lebih lemah (lebih besar) dari N; yaitu dimana Batas atas lemah ini, yang diatributkan pada beberapa karya Graham tak terpublikasikan, sebetulnya dipublikasikan (dan diperlakukan sebagai bilangan Graham) oleh Martin Gardner dalam [Scientific American, "Mathematical Games", November 1977].
Definisi bilangan Graham
Dengan menggunakan notasi panah-atas Knuth, bilangan Graham G adalah

dimana banyak tanda panah pada tiap lapis, mulai dari lapisan atas, ditentukan oleh nilai pada lapisan berikutnya dibawahnya; yaitu


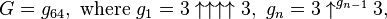
Penjelasan yang lebih simple :

Graham's Number ini berkaitan dengan pangkat... coba... 3^3 berapa? jawabanyya pasti 27 kan? karena 3x3x3.

nah kalo Graham's Number.. itu lambang " ^ " / pangkatnya banyakk bangett

3^3 = 3x3x3 = 27
kalo 3^^3 ?? nah lo ?

3^^3 = 3^ (3^3) = 3^27 = 7,625,597,484,987
 kalo 3^^^3 ?? nah lo ?

3^^^3 = 3^^(3^^3) = 3^^7,625,597,484,987 = 3^(7,625,597,484,987^7,625,597,484,987) 
kalo 3^^^^3 nah lo ?

3^^^^3 = 3^^^(3^^^3) = susah diitung ...!!!
 nah ini dia...
3^^^^3 itu sama dengan G1. ( ibarat G1 itu hanya sebuah lambang...)

jadi G1 = 3^^^^3
kalo G2 = 3^^^^.........^^^3 ( pangkatnya sesuai dengan G1)
 kalo G3 = 3^^^^^.......^^^^3 ( pangkatnya sesuai dengan G2 )

nah Graham's number itu saat G64. jadi lakukan seperti yang diatas hingga 64 kali... jadi

G64 =3^^^^^.........^^^^^3 (pangkatnya sesuai dengan G63 )
nah lo? gede buangettzzzzzzz kan??????
nih biar langsung to the point. Graham's Number = G64 =3^^^^.....^^^^^^3 (sesuai dengan pangkat G63 )
jadi gini nih G64 = 3^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^......................dst

BACA : 3 pangkat pangkat pangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkatpangkat pangkat dst.......



Udah ngerti kan??




Sekian dulu informasi dari saya, info lebih lanjut, tanyakan di google :D
 
Tambahan : 500 digit terakhir G64
02425950695064738395657479136519351798334535362521
43003540126026771622672160419810652263169355188780
38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080
25459461494578871427832350829242102091825896753560
43086993801689249889268099510169055919951195027887
17830837018340236474548882222161573228010132974509
27344594504343300901096928025352751833289884461508
94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387